Chapter 9
(AST301) Design and Analysis of Experiments II
9 Additional Design and Analysis Topics for Factorial and Fractional Factorial Designs
9.1 The
The three-level design is written as a
These are (usually) referred to as low, intermediate and high levels. These levels are numerically expressed as 0, 1, and 2.
One could have considered the digits -1, 0, and +1, but this may be confusing with respect to the 2-level designs since 0 is reserved for center points. Therefore, we will use the 0, 1, 2 scheme.
A third level for a continuous factor facilitates investigation of a quadratic relationship between the response and each of the factors.
Each treatment combination in the
For example, in a
In the
Regression model for analyzing
The
- response surface design
The
The
- Main effect of
- Main effect of
- Interaction
For
The sums of squares for the effects
The two degrees of freedom of each main effect can be represented by a linear and a quadratic component each with a single degrees of freedom. Suppose that both factors
The two-factor interaction
Dividing
The second method is based on the orthogonal Latin squares. Two Latin squares are said to be orthogonal if one square is superimposed on the other, produce all possible ordered pairs of symbols exactly once.
Example 5.5
The effective life of a cutting tool installed in a numerically controlled machine is thought to be affected by the cutting speed and the tool angle. Three speeds and three angles are selected, and a
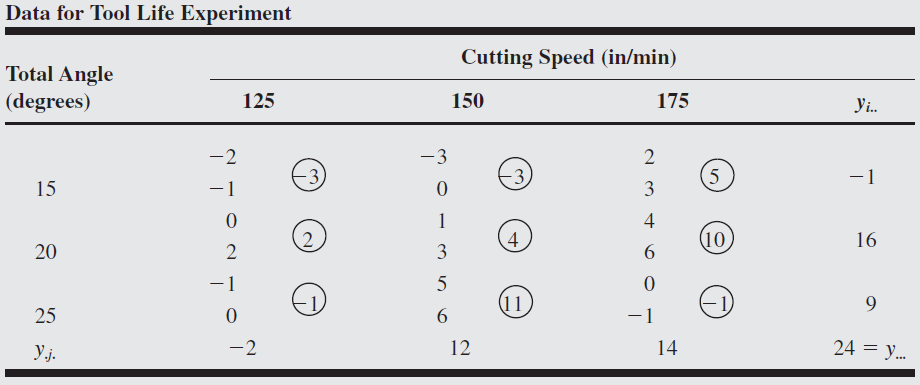
Since the factors are quantitative, and both factors have three levels, a second-order model such as
From the data we obtain sum of squares as
The second method is based on orthogonal Latin squares. This method does not require that the factors be quantitative, and it is usually associated with the case where all factors are qualitative.
The two factors
For the above example, two particular
Treatment combination totals from Example 5.5 with two orthogonal Latin squares superimposed
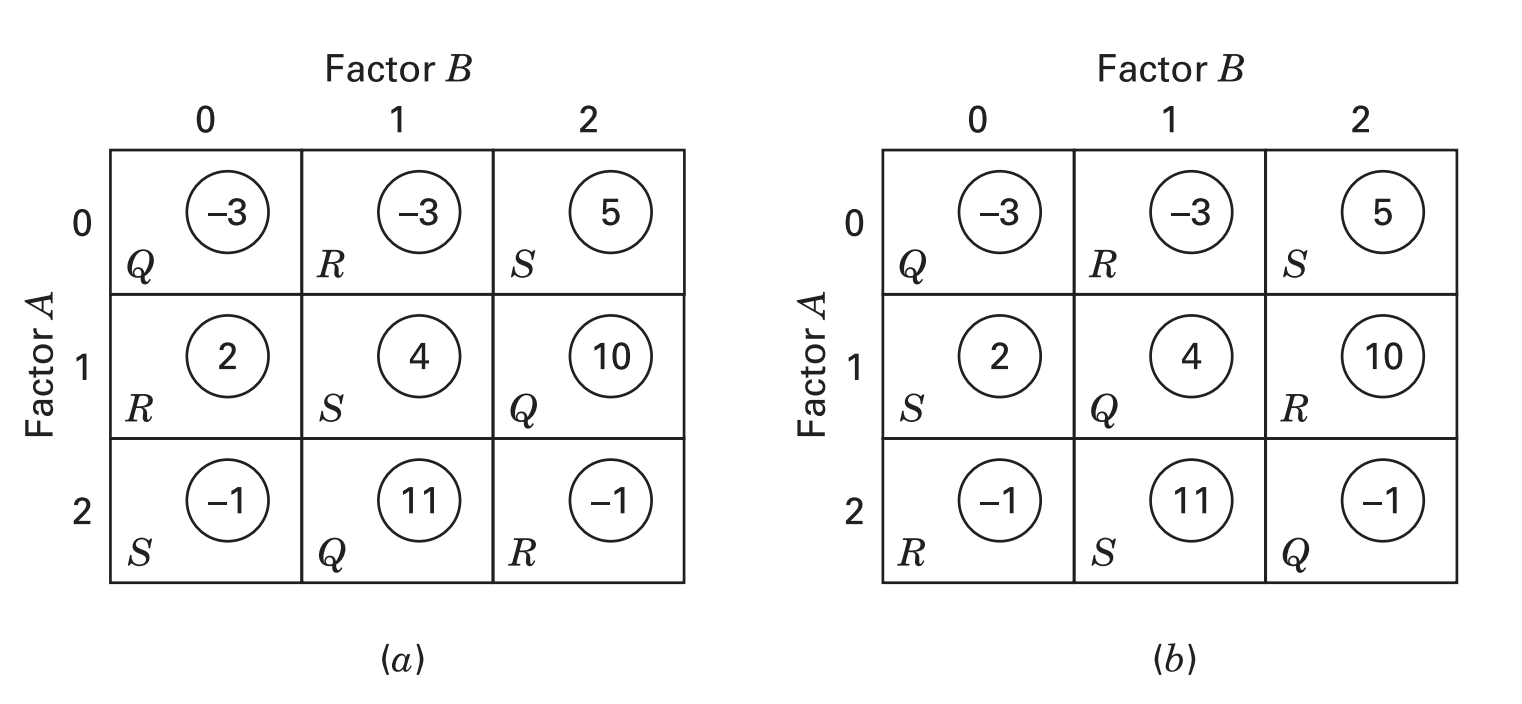
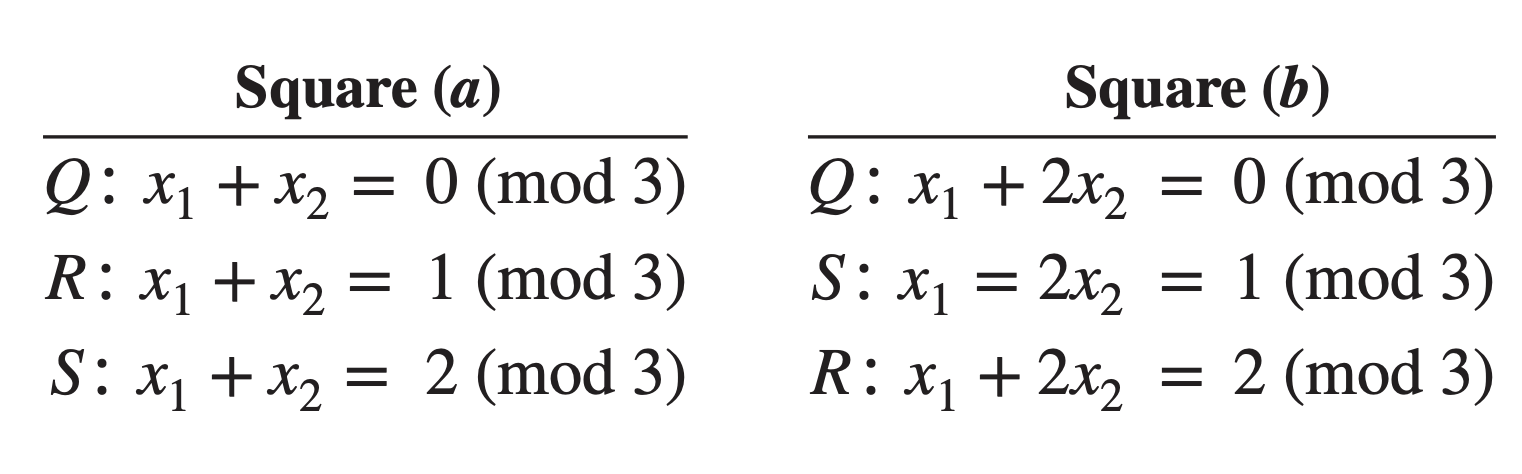
So, SS from first table is known as
Total of the letters from the first table:
Total of the letters from the second table:
It can also be shown that
There is another way of calculating the
Add the data by diagonals downward from the left to right and the totals are
Add the data by diagonals downward from the right to left and the totals are
Yates called these components of interaction as the
The
The
Among 26 degrees of freedom, 6 for the main effects, 12 for the two-factor interactions, and 8 for the three-factor interaction
For
Sums of squares can be calculated using the standard methods, in addition to that, if the factors are quantitative
- Main effects can be partitioned into linear
- Two-factor interactions can be partitioned into components corresponding to
- Three-factor interaction can be partitioned into components corresponding to
The sum of squares corresponding to the two-factor interaction has
The sum of squares corresponding to a three-factor interaction has
The general
The
There are
- one
If there are
Sums of squares for different effects are computed by usual method of factorial design
Any
E.g. The four-factor interaction
Note that only exponent allowed for the first letter is 1 and if the exponent of the first letter is not 1 then the entire expression must be squared, e.g.
These interaction components have no physical meaning but they are useful in constructing more complex designs
9.2 Confounding in the
Even when a single replicate of the
Thus, confounding in blocks is often necessary. The
Thus, these designs may be confounded in three blocks, nine blocks, and so on.
The
The three blocks have two degrees of freedom, so there must be two degrees of freedom confounded with blocks
In the
- each main effect has two degrees of freedom
- each two-factor interaction has four degrees of freedom, which can be decomposed into two components (e.g.
- each three-factor interaction has eight degrees of freedom, which can be decomposed into four components (e.g.
- and so on
So it is convenient to confound an interaction component with blocks
The general procedure to construct a defining contrast
- For
- Suppose goal is to construct a
- If
- The value of
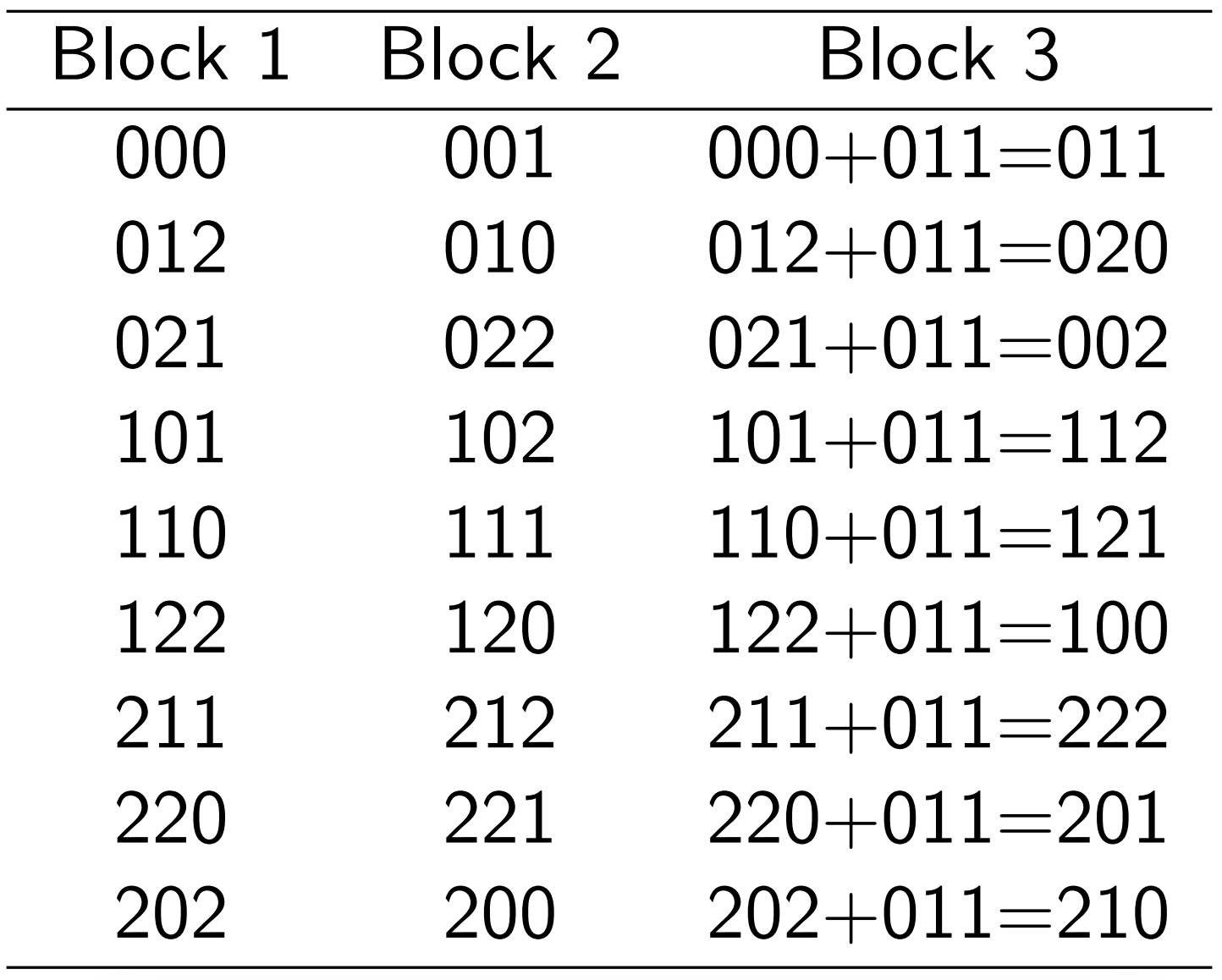
Assignment of treatment combinations to blocks
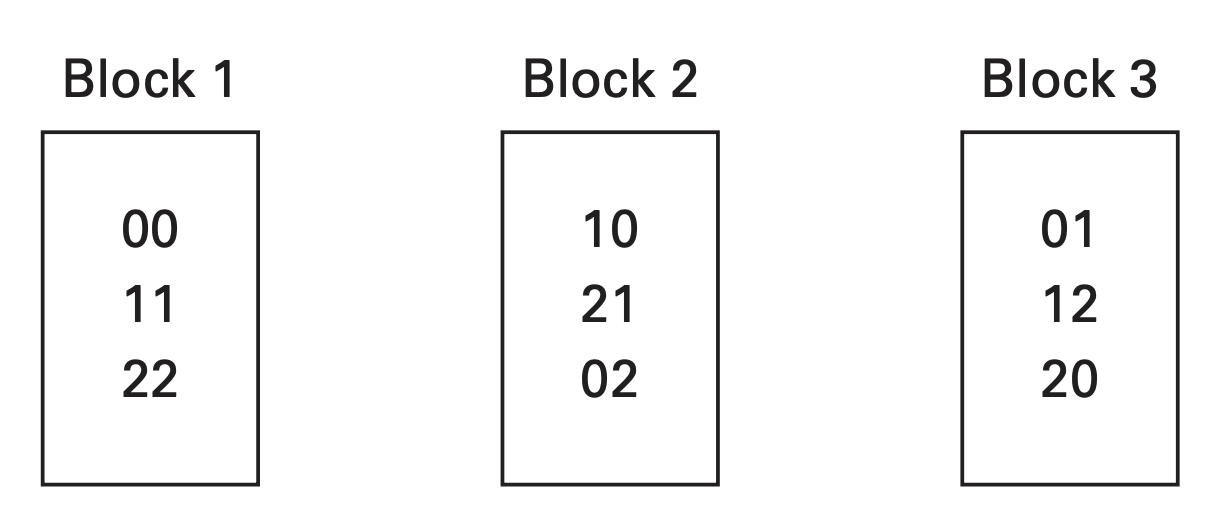
Note that the treatment combinations of principal block form a group with respect to addition (mod 3), i.e. addition of pair of treatment combination will lead to a treatment combination of the principal block. E.g.
Assignment of treatment combinations to blocks

Note that the treatment combinations in the other two blocks may be generated by adding (mod 3) any element of the new block to the elements of principal block. E.g.
Example 9.2
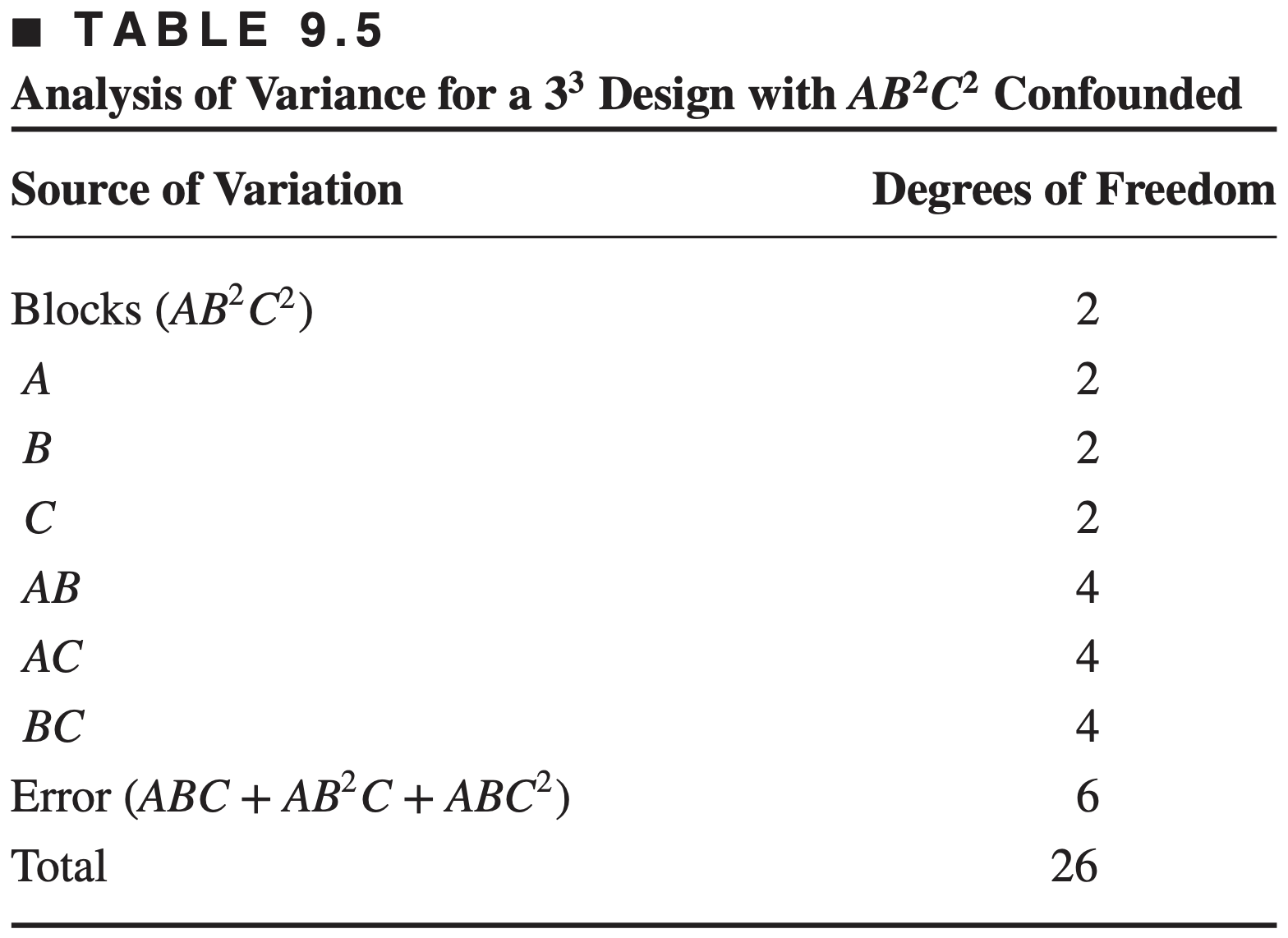
The statistical analysis of the
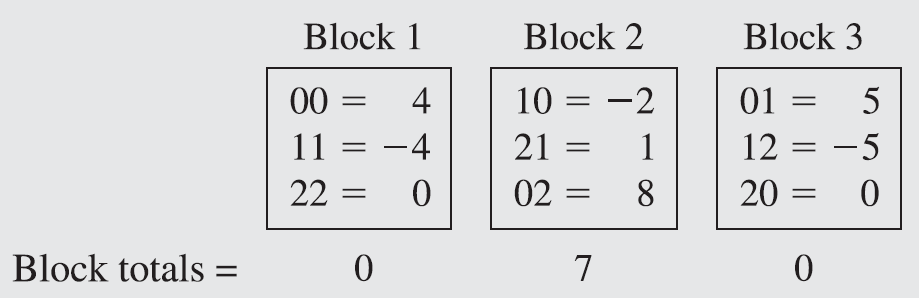
We find that
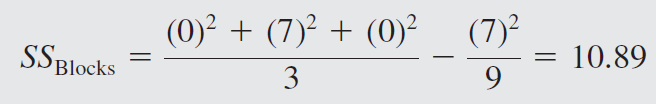
SS for main effects and interaction: 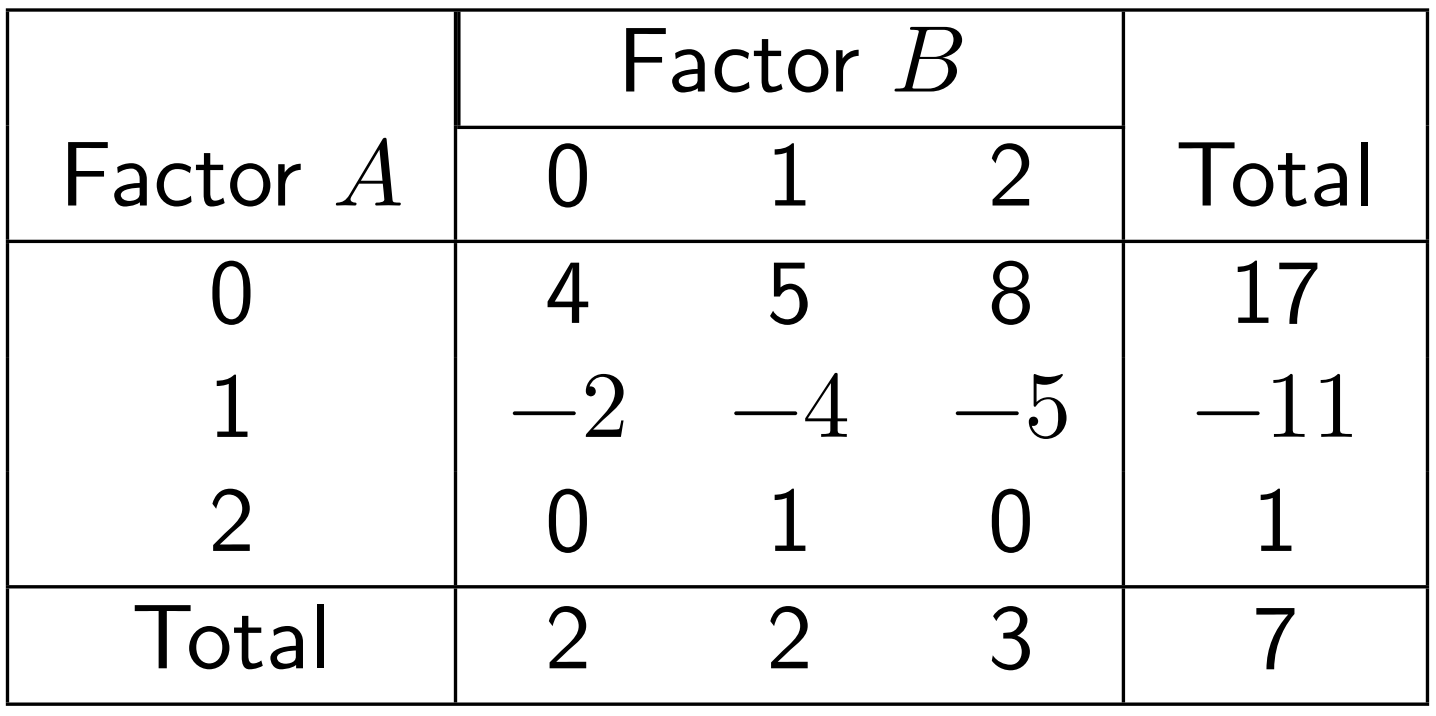
The I or
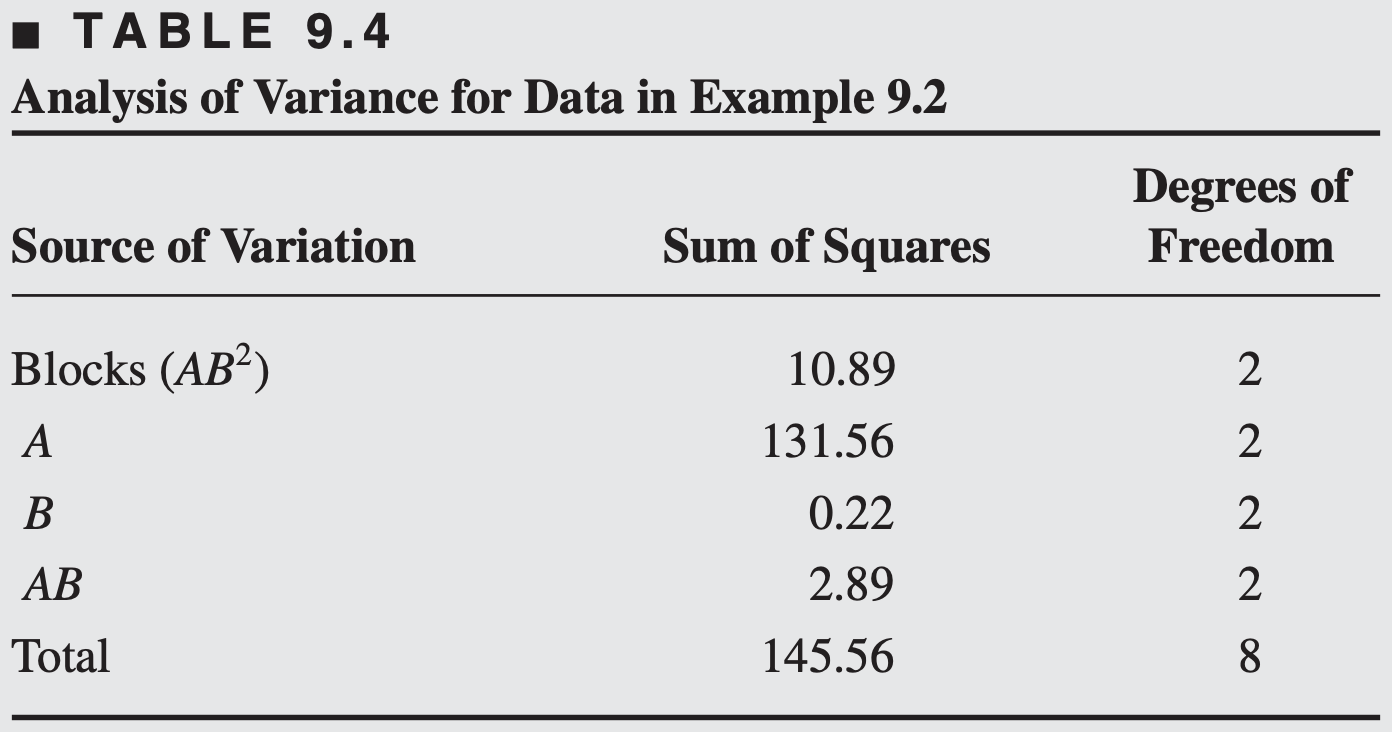
The analysis of variance is shown below. Because there is only one replicate, no formal tests can be performed. It is not a good idea to use the AB component of interaction as an estimate of error.
Slightly complicated example: The
Treatment combinations of the principal block of the
Treatment combinations of other two blocks can easily be obtained by adding a treatment combination (which is not in the principal block) to each element of the principal block
The
- If
- We need to choose two interaction components (4 degrees of freedom), which will result two more components will be confounded (4 degrees of freedom)
- E.g. if
- There will be two defining contrasts
Consider the
Suppose we choose to confound
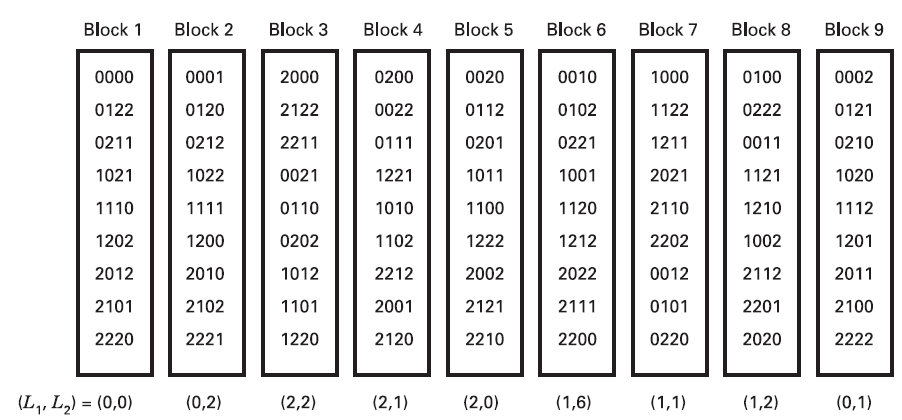
9.3 Fractions of
The one-third fraction of the
The largest fraction of the
To construct a
Each of the three resulting blocks is a
If
The alias structure for an effect can be obtained by multiplying the effect by both
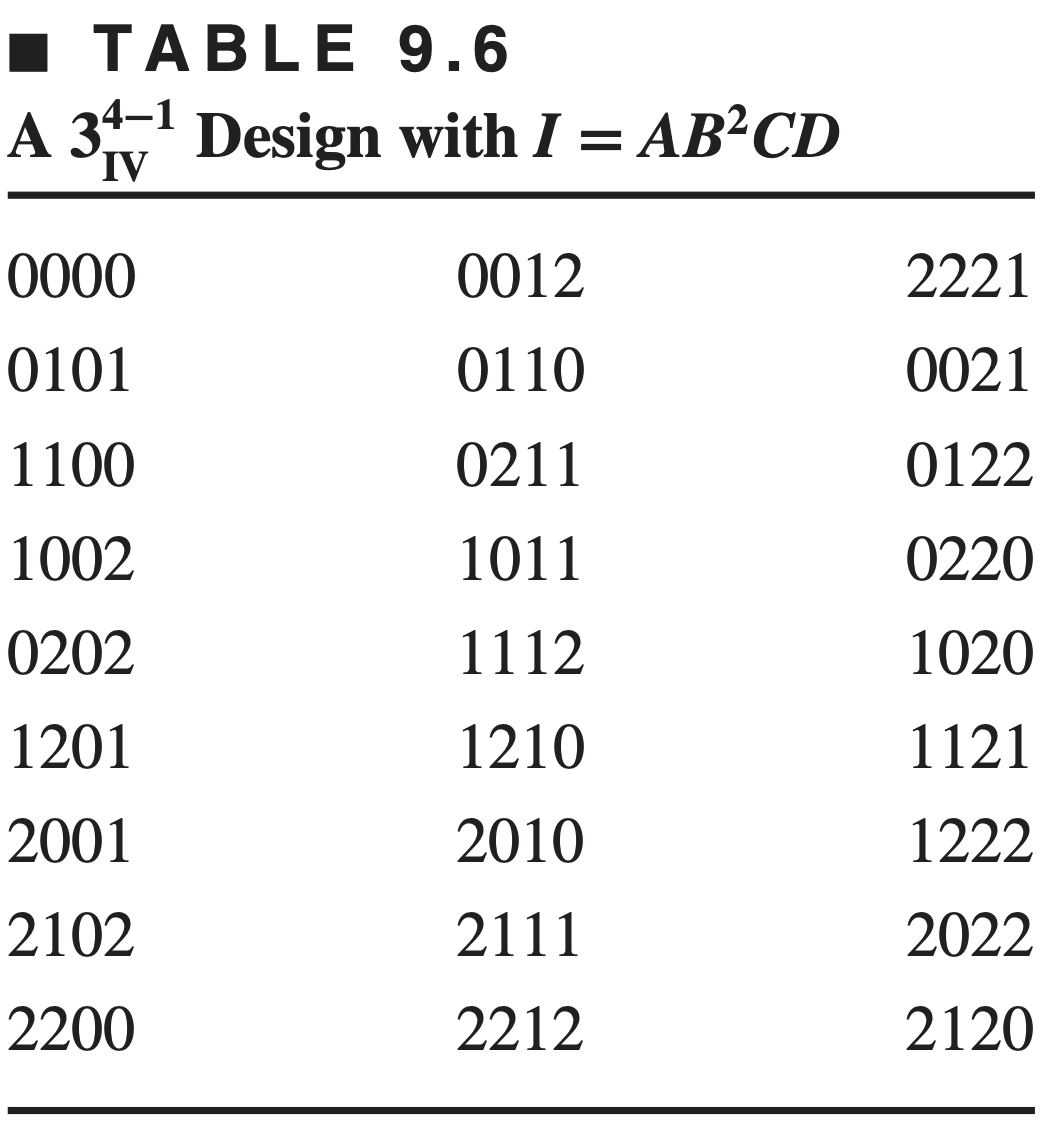
- Example: To construct a one-third fraction of the
- Since there are four interaction components, which are
- If we select the component
The alias structure with the defining relation 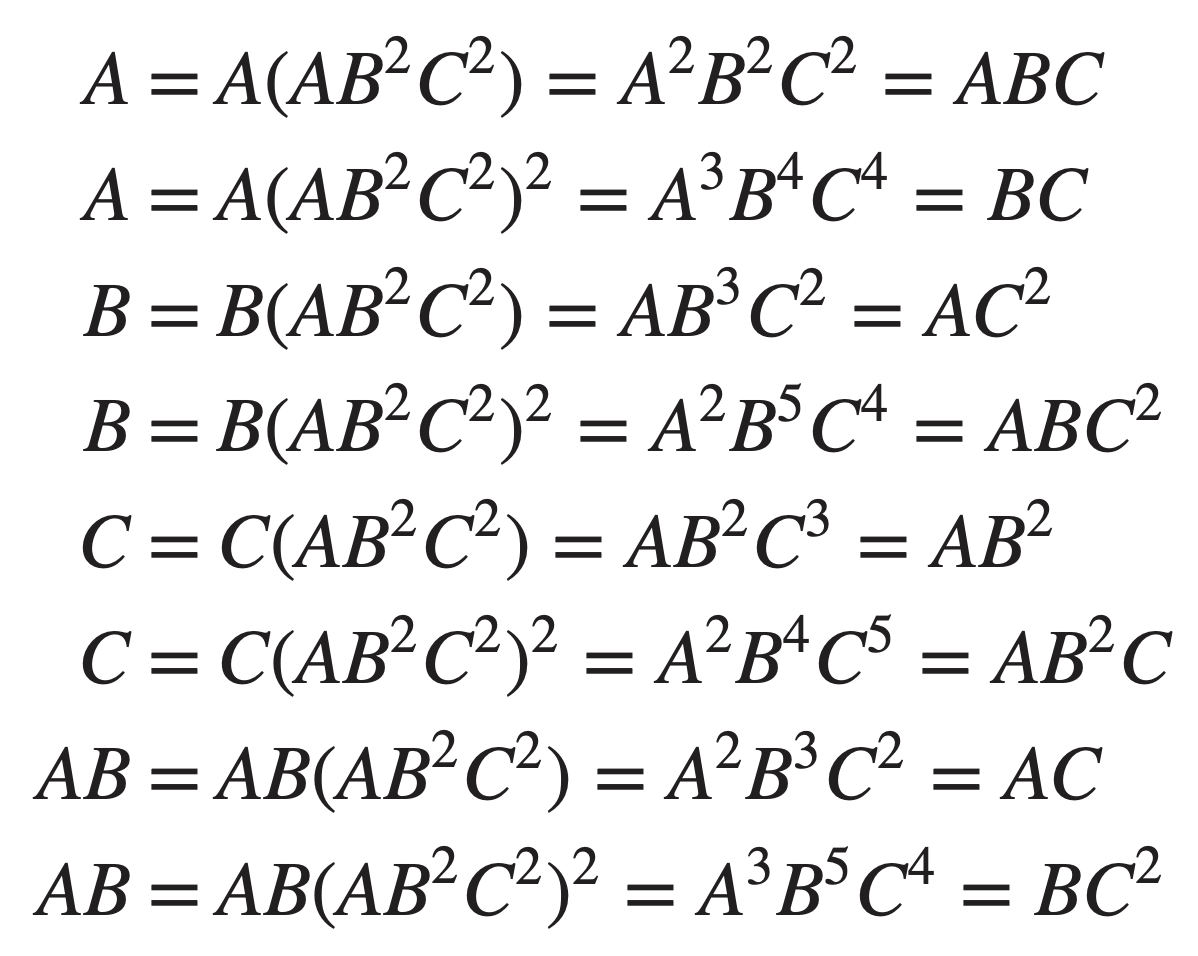
The four effects that are actually estimated from the eight degrees of freedom are:
The treatment combinations in a
- Write down the
- The
Consider a one-third fraction of the
First construct the 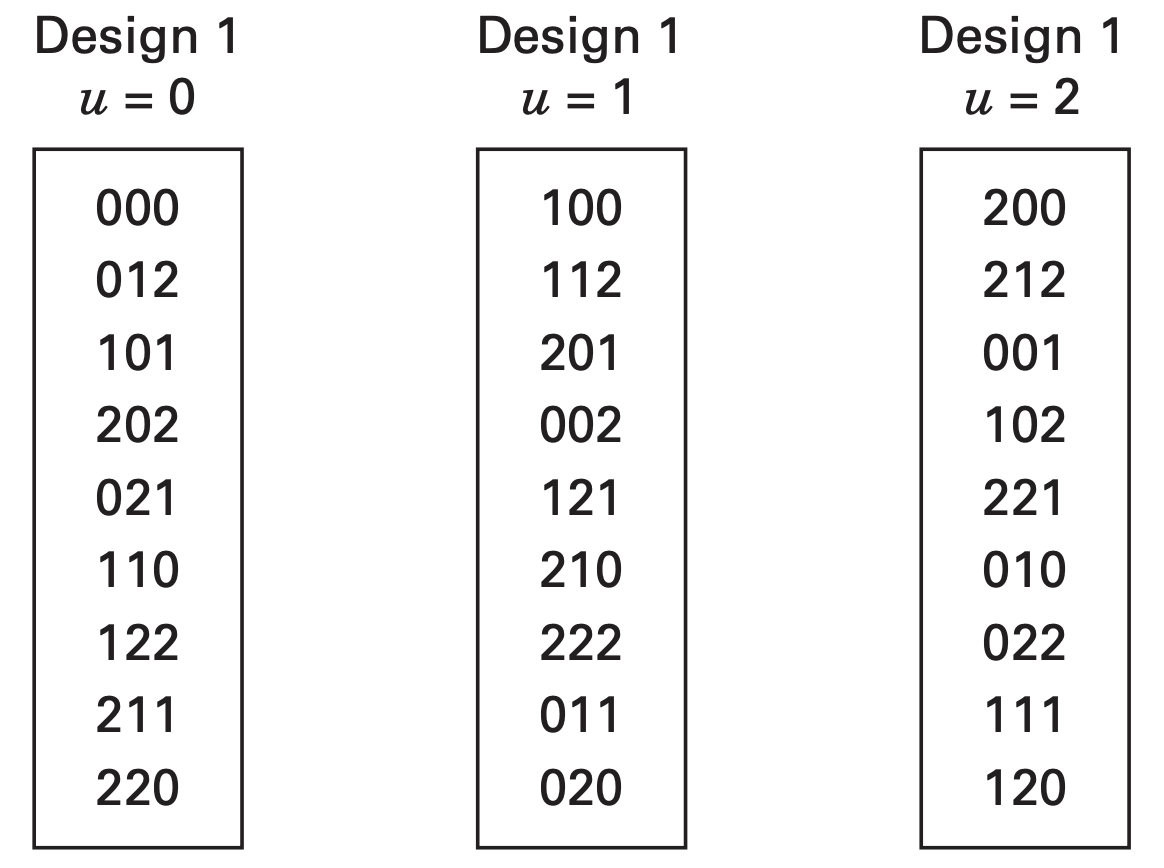
Levels for the factor
Defining relation:
As an example, alias structure for the effect
Resolution??
The general
- The
- The construction of
- The defining relation
- Alias structure of an effect can be obtained by multiplying the effect by the defining relation
- The